The Conceptual History of Black Holes
- William Wolf
- Jan 3, 2021
- 6 min read
It has been quite a decade for Einstein’s general theory of relativity. From LIGO detecting gravitational waves from inspiraling black holes to the EHT capturing an image of the event horizon of the super massive black hole at the center of the galaxy Messier 87, the last several years have provided striking confirmation for Einstein’s theory. These fabulous discoveries unexpectedly have resulted in multiple Nobel Prizes the most recent of which was awarded to Oxford’s own Sir Roger Penrose for his use of “ingenious mathematical methods in his proof that black holes are a direct consequence of Albert Einstein’s general theory of relativity”[1, 2]. It is well known that the very concept of a “black hole” went from being ridiculed by Einstein himself as preposterous to an empirically confirmed phenomena recently thanks in large part to Penrose’s work that convinced the physics community of their reality all while capturing the popular imagination in works of science fiction. What is less well known is that the idea of a “black hole” has been around much longer than even Einstein and can trace its roots back to the works of mathematicians and physicists in the 1700s [3][4]. An argument for their existence can be demonstrated with a surprisingly simple scenario using nothing more than basic Newtonian mechanics and has a number of parallels with the modern understanding of black holes.
John Mitchen and Pierre Simon Laplace both were inspired by corpuscle theories of light meaning that they - like Newton - believed light was made of tiny particles. Even though we now know light is massless, it made sense back then to consider what might happen to the presumably massive particles that constituted light if they were placed under the influence of gravity. This will involve writing down an equation, but a simple one at that! Consider the following:
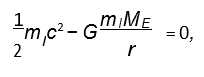
Recall that forces are very important in physics and will determine the motion of objects. Imagine a situation where we have an object that has two forces acting on it but that these forces are in opposite directions. If they are exactly equal we can also say that the energies imparted to the object and caused by the relevant forces will be equal as well. Now imagine this situation for a massive particle of light where it has the energy that is propagating it forward, but this is being opposed by gravity tugging on it in the opposite direction. The equation above describes the sum of the kinetic and potential energy of a massive particle of light ml released from the surface of the earth that travels at the speed of light c that is being tugged on by the gravity of earth ME which is a spherical body with a radius r. The equation above is set to zero because any time an object is trying to escape a gravitational field it must go against the force of gravity. The sum of kinetic and potential energy being zero just describes what the minimum positive kinetic energy needed to escape and overcome the negative potential energy of gravity is. For example, if we launch a rocket from the surface of the earth and its velocity is large enough that its kinetic energy is larger than the potential energy of gravity holding it down the rocket will escape the earth and get into space rather than crashing back down to the surface. Essentially, if the sum in the first equation is positive the object escapes, but if it is negative the object comes back down. Zero is when the situation is hanging in a balance between those two outcomes.
What happens to one of these light corpuscles when we are in this situation hanging in the balance? We know light is very energetic and gravity would have to be very powerful to capture it. We also know that ml will not matter because we can factor it out of the equation and G is a constant. This means that in order for gravity to be powerful enough to capture light (given by the sum of the energies being either less than or equal to zero) the ratio of ME and r must be really large. Essentially, we would need to have a lot of mass packed into a small radius which is a very common notion of what leads to a black hole! We can rearrange the first equation to find the radius r = 2GME . This turns out to be the famous Schwarzchild radius that you find when you do all the (much more complicated) relativistic calculations! And we found it by doing nothing more than considering a very simple system from Newtonian mechanics.
A system satisfying these relationships describes a situation where the amount of mass packed into a relatively small radius would lead to gravity being so powerful that light corpuscles couldn’t escape thus giving us a “dark star” or “black hole” - invisible to our eyes, but potentially lurking in space. It turns out that when we do all the relativistic calculations this Schwarzchild radius causes a singularity where the full equations diverge to infinity and become undefined. This is problematic because our best physics theories shouldn’t break down and become undefined in this way! Even Einstein couldn’t accept singularities and provided arguments to the effect that they “do not exist in reality” [5]. One of the most popular reasons for believing this was that any arguments for the existence of black holes to that point relied on very special circumstances. Our Newtonian argument is an incredibly idealized scenario in that we assumed perfect spherical symmetry in the problem and is obviously incorrect because light does not have mass, but even the Schwarzchild solution seems very unrealistic because obtaining this solution relies on perfect spherical symmetry which certainly does not exist in nature. If we could actually solve the equations in a realistic scenario surely these annoying singularities would disappear? This is where Penrose comes into the picture.
Penrose introduced the notion of a “trapped surface” to our study of relativity and this effectively generalizes what we were saying earlier about gravity being so strong that it can trap light. His singularity theorems can get pretty complicated, but we can get a decent intuitive understanding of what is going on by considering a description given by his close collaborator Stephen Hawking in his book “The Large Scale Structure of Space-Time” [6]. Consider a sphere surrounding a massive body. Imagine this sphere emits two pulses of light PI and PO. PI is directed inwards and PO is directed outwards. Normally we would expect the area enclosed by light from PI directed inward to become smaller with time as the light rays converge on each other while the area enclosed by the light from PO directed outward will grow larger as the light rays move away from each other and spread out in space. But wait! Remember that very strong gravitational fields bend space and will affect the path that these light rays take. If there is enough mass contained within this region the resulting curvature will be such that the path these light rays traverse will behave in a very strange way. That is, the two areas enclosed by PI and PO will both become smaller as time goes on even though the pulse PO was directed outward.
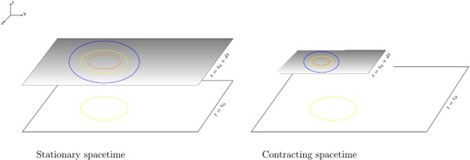
Figure 1: This illustration compares what happens to the two pulses of light as time passes under normal circumstances vs circumstances that involve a trapped surface [7]
Essentially, the curvature caused by the mass in the region is so strong that the light rays can’t spread out away from each other and the curvature directs their paths to converge into ever smaller areas. In other words, a black hole has formed and this generalizes the earlier ideas we considered before about gravity trapping light. Notice also that even though we used this analogy of spheres of light to communicate the general idea, this argument doesn’t depend on symmetries. At no point did we ever mention the mass in the region being a spherical body and it turns out that the arguments that Penrose put forth (in their full mathematical glory) don’t depend on this mass distribution behaving in a particularly convenient or idealized manner. These trapped surfaces form without any of these simplifying assumptions!
Roger Penrose’s contributions to this field were immense and convinced the physics community that black holes were objects that we needed to take seriously almost overnight. This inspired both theorists and experimentalists in the following decades to pursue the study of these objects and many of the fabulous results that have come out recently owe a huge debt of gratitude to Penrose. Finally, these mysterious, seemingly fantastical objects that were conjectured hundreds of years ago in the context of Newtonian physics and then came up again when Einstein published his theory of gravity now had a rigorous and convincing argument for their existence even in physically realistic situations.
Author: William Wolf, Philosophy, Merton College
References
[1] The Royal Swedish Academy of Sciences. Press release: The nobel prize in physics 2020. 2020.
[2] The Nobel Committee for Physics. Scientifc background on the nobel prize in physics 2020. 2020.
[3] Pierre Simon Laplace. Exposition du Syst`eme du Monde. 1796.
[4] John Mitchell. On the means of discovering the distance, magnitude, c. of the fixed stars, in consequence of the diminution of the velocity of their light, in case such a diminution should be found to take place in any of them, and such other data should be procuredfrom observations, as would be farther necessary for that purpose. 1783.
[5] Albert Einstein. On a stationary system with spherical symmetry con- sisting of many gravitating masses. The Annals of Mathematics, 1939.
[6] S.W. Hawking and G.F.R.Ellis. The Large ScaleStructure of Space-Time. 1973.
[7] Jos´e M. M. Senovilla and David Garfinkle. The 1965 Penrose singularity theorem. Class. Quant. Grav., 32(12):124008, 2015.
Comments